“坏了坏了，卡特林那巡天系统刚刚发现了一颗五公里大小的小行星，NASA JPL 用他们的数据算了一下这颗小行星的轨道，它将在一年后撞上地球！”
“什么！一年后？之前怎么会没发现它呢？五公里大小的近地小行星应该早就被自动巡天系统发现到了才对啊？”
”这怎么知道？IAU 刚刚也公布了这颗小行星的名字——Shito（使徒），看来人类这次是真的完蛋了……“
”现在哪还有时间搞命名这种虚头巴脑的事情啊，而且为什么会用 EVA 里的角色给小行星命名啊！现在得赶紧想办法啊。快，把小行星的轨道数据传给我，我来算算人类还有没有存活下去的希望。“
”呜呜呜，我把数据发给你了，这次只能靠你了“
使徒袭来！
（EVA BGM 开始响起）
现在，为了拯救人类，你必须在最短的时内设计出一套可行的地球防御方案，然后把它提供给刚刚成立「行星安全理事会」。人类这次能否逃过一劫，就完全掌握在你的手中了！
你收到了助手传来的小行星数据。喝！这颗名叫使徒的小行星直径约 5 公里，你回忆起来小行星的密度大约是 \(2000\ kg/m^3\)，那么它的质量就应该是：
\[M = \frac{4}{3}\pi R^3 \rho = 1.31\times10^{14} \ kg\]这可是 1.3 千亿吨的物质朝着地球飞过来啊。如果撞上的话，人类就会像当初恐龙那样全体从地球表面消失了。
你先看了看使徒的轨道根数：半长轴 1 AU（AU = 天文单位，即日地距离）、偏心率和倾角都是 0，就像是谁提前设计好的一样！
现在使徒正在近距离飞跃地球，JPL 预测它将在一年后撞上，也就是说它下一次与地球的重逢就将是人类的审判之日！
不过你同时也松了一口气：现在使徒离地球的距离很近，这意味着我们在很短的时间窗口发射航天器来实施改变小行星轨道的计划，甚至可以派驻宇航员到小行星表面进行操作！
你立马在脑海中搜寻着最有可能改变小行星轨道的方法：
动能撞击？
不可能，这颗小行星的质量太大，想要用人类现有航天器那点可怜的质量来改变使徒的速度无异于蚍蜉撼树。
引力牵引？
更别想！引力牵引只能适用于提前预警了很多年的小行星，这种还有一年就撞上、质量又大的”奇行种“怎么可能牵引得动啊！
你思来想去，只能祭出现今人类的最强核能武器：氢弹了。
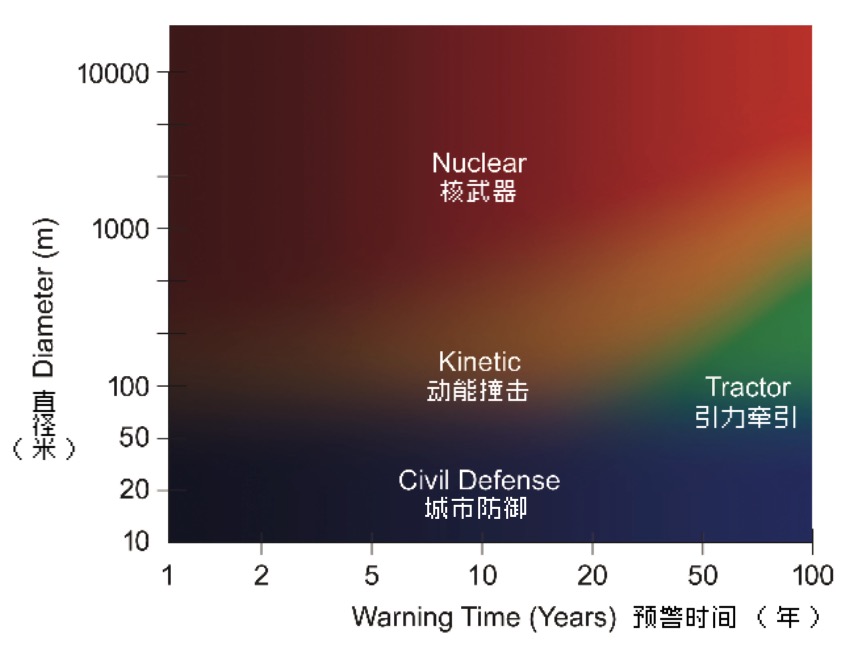对于不同预警时间和大小的小行星，人类能采取的措施示意图
确定了防御措施之后，你赶紧拿出纸和笔，开始计算需要多少颗氢弹才能让使徒偏离预定航线！
轨道计算？就包在我身上了！
你先整理整理目前知道的信息：使徒和地球有着非常相似的轨道：它们的半长轴都是 1 AU，偏心率和倾角都接近于 0。如果不改变使徒现有轨道，那么根据 JPL 的计算，它将在一年后，也就是一个轨道周期后撞上地球！
你现在假设改变轨道后的使徒所具有的半长轴为 \(a_* = a + \Delta a\)，其中 \(a\) 是地球轨道半长轴，\(\Delta a\) 是半长轴增量。
那么使徒轨道和地球轨道的平均运动速率之差为：
\[\Delta n = n - n_*\]你回想起了开普勒第三定律， \(\frac{2\pi}{P} = n = \sqrt{ {GM}\over{a^3}}\) ，那么：
\[\begin{align*} n_* &= \sqrt{ {GM}\over{a_*^3}} \\ &= \sqrt{ {GM}\over{(a+\Delta a)^3}} \\ &\approx \sqrt{ {GM}\over{a^3}} - \frac{3}{2} \sqrt{ {GM}\over{a^3}} \frac{\Delta a}{a} \end{align*}\]比较这个式子和关于 \(\Delta n\) 的式子，你发现：
\[\Delta n = \frac{3}{2} n \frac{\Delta a}{a}\]而使徒能偏离多少地球距离完全取决于这个 \(\Delta n\) 的大小！假设我们需要使徒在一年后（ \(T\) ）轨道偏离 \(N\) 倍的地球半径（\(R_\bigoplus\)），那么它们之间的关系是：
\[N R_\bigoplus = a \Delta n T = \frac{3}{2} n \Delta a T\]你开始思考，要产生 \(\Delta a\) 的半长轴增量，我们需要现在给使徒提供多少的速度增量，也就是 \(\Delta v\) 呢？
你回忆起了轨道速度和半长轴的关系：
\[v^{2} = \frac{GM}{a}\]对于速度上的小扰动 \(\Delta v\) ，我们有：
\[2 v \Delta v= - \frac{GM}{a^2} \Delta a\]使用上面这个式子替换 \(\Delta a\)，就得到了：
\[N R_\bigoplus = -{ {3n v a^2 T } \over {GM}} \Delta v\]注意到：
\[n v = \sqrt{ {GM \over a^3}} \sqrt{ {GM \over a}} = {GM \over a^2}\]整理之后，你最后得到这个公式：
\[N R_\bigoplus = -3 T \Delta v\]其中 \(N R_\bigoplus\) 是要偏离几倍地球半径， \(T\) 是改变使徒轨道的时间， \(\Delta v\) 是你需要的速度增量。
这个时候，你的助手走了过来，他看着你草稿纸上的公式，难掩着自己的兴奋之情向你说道：
”哦哦，我看明白了！现在只需要把 \(N = 1 ， T = 1 \ yr\) 带入到公式，就可以算出我们需要的 \(\Delta v\) 了吧！“
你开始思考助手提出问题：在最坏的情况下，使徒会撞上地球的正中央。这个时候，是不是只要让使徒偏离一倍地球半径就能够化解人类的危机呢？
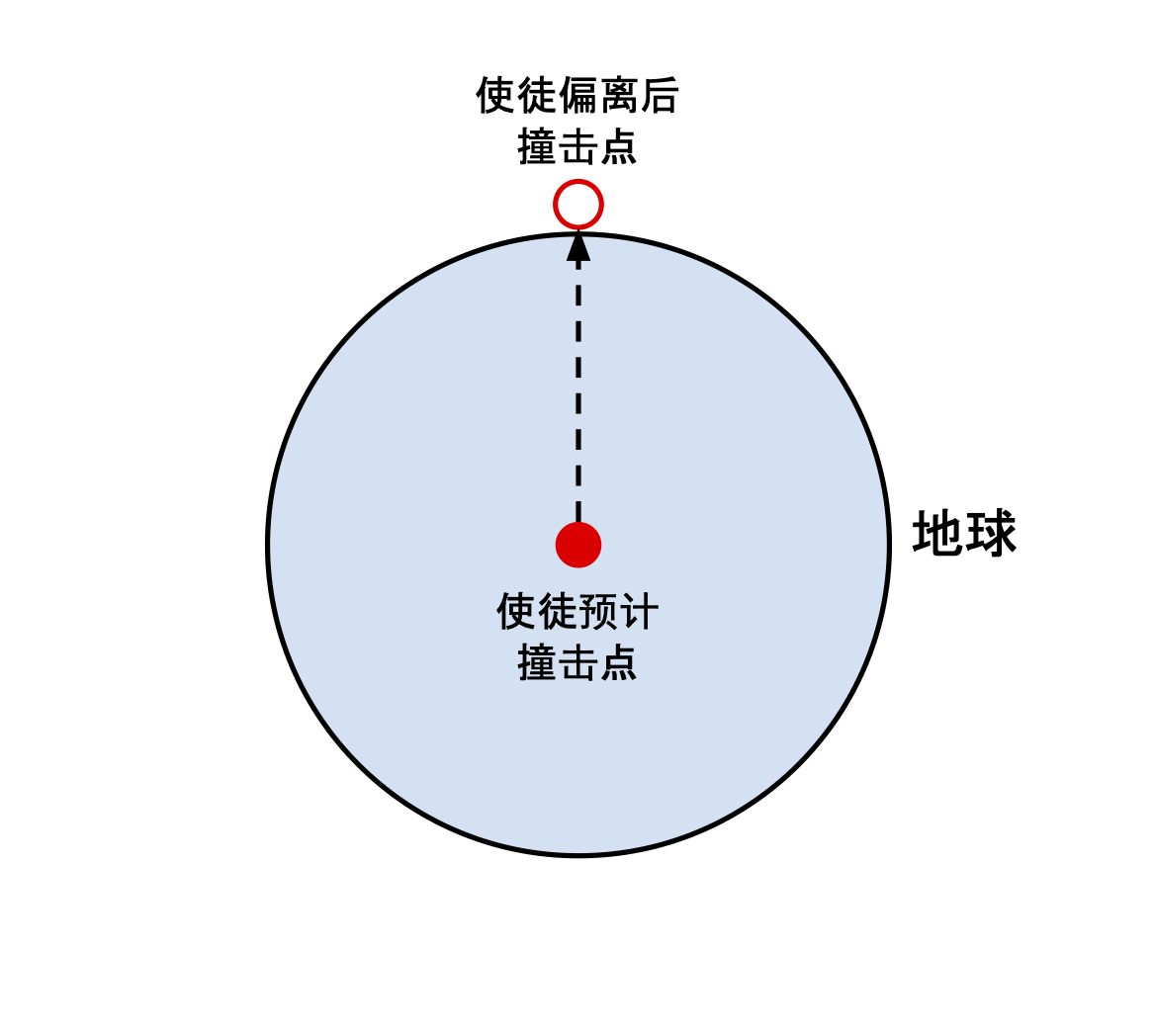「使徒袭来」示意图，未考虑地球引力的影响
不是的！
你的助手忽略了一个致命的事实，那就是地球的引力会让使徒的潜在撞击半径变大！！
深吸一口气之后，你又开始了挑灯夜战……
我的回合！引力陷阱卡发动！
在助手传来的关于使徒的数据中，有一条引起了你的注意：
使徒将会以 9 公里/秒的速度撞向地球！
这指的应该是使徒进入地球希尔球之后的相对速度，而不是地球撞上地球时的速度。因为你记得，地球的逃逸速度为 11.2 km/s，而小行星撞上地球的速度只能会比逃逸速度大！
你在草稿纸上画出了示意图：
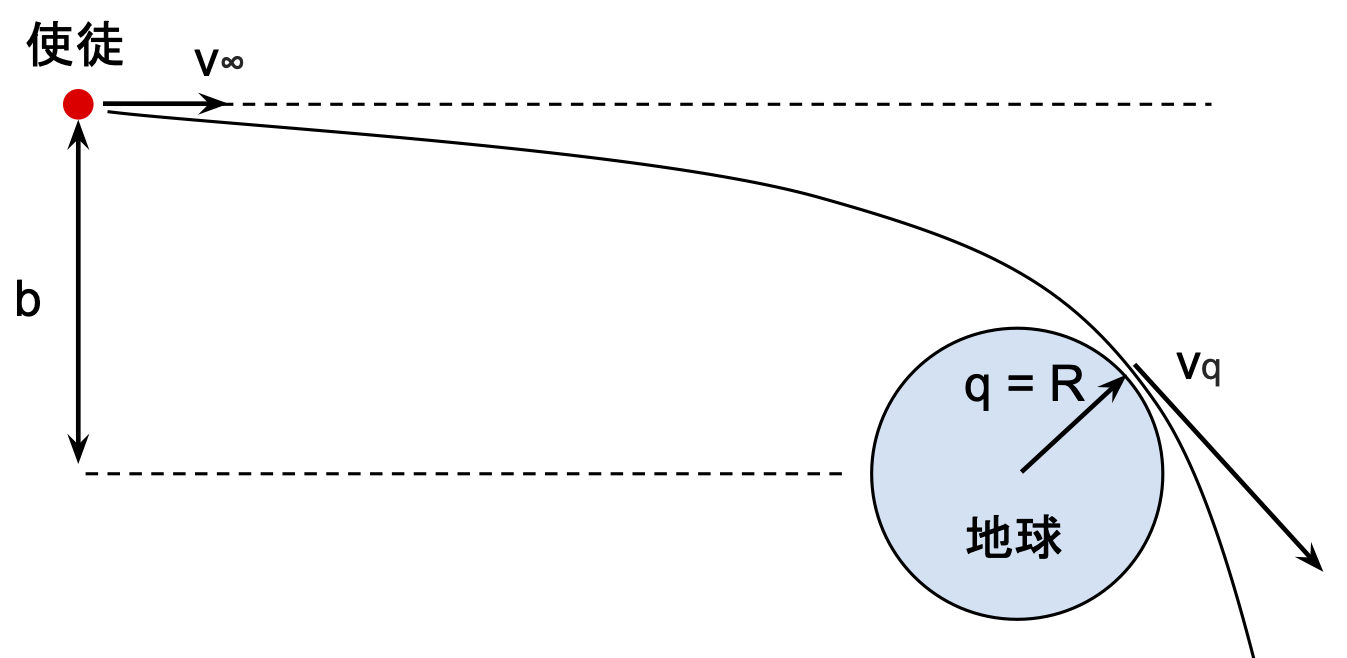地球的”引力聚焦“效应
你知道，由于地球引力，使徒在进入地球希尔域之后将沿着双曲线轨道飞掠地球。而一旦这条双曲线轨道的近地点 \(q\) 小于地球半径 \(R_\bigoplus\) ，使徒就会撞上地球的背面。换句话讲，地球自身的引力让潜在碰撞半径变大了，这也被称作地球的”引力聚焦（Gravitational focusing）“效应。
现在，你要计算的就是，对于相对速度为 \(v\) 的小行星，地球的引力聚焦效应究竟有多大？
你想起来，使徒在飞跃时，其相对于地球的能量和角动量是守恒的！
根据能量守恒：
\[\frac{1}{2} v_\infty^2 = \frac{1}{2} v_q^2 - \frac{GM}{q}\]其中 \(v_\infty\) 为进入希尔域时，使徒相对于地球的速度； \(v_q\) 是近地点速度。
根据角动量守恒：
\[bv_\infty=qv_q\]联立两式，你可以解得：
\[{ {b^2}\over{R_\bigoplus^2} } = 1 + \frac{2GM}{v_\infty^2 R_\bigoplus}\]你想起来，地球表面逃逸速度的定义式正是 \(v^2_{esc} = \frac{2GM}{R_\bigoplus}\) ，因此：
\[b = R_\bigoplus \sqrt{1+\frac{v_{esc}^2}{v_\infty^2}}\]而式子中的 \(\sqrt{1+\frac{v_{esc}^2}{v_\infty^2}}\) 被称作行星的引力聚焦系数。这个系数表征了地球会因为自身引力”变胖“多少。
你意识到，在计算要使徒偏离多少倍地球半径时，必须得考虑地球的引力聚焦效应。否则的话，就算让它偏离一倍半径，使徒还是会撞击到地球背面，你的努力就会功亏一篑：
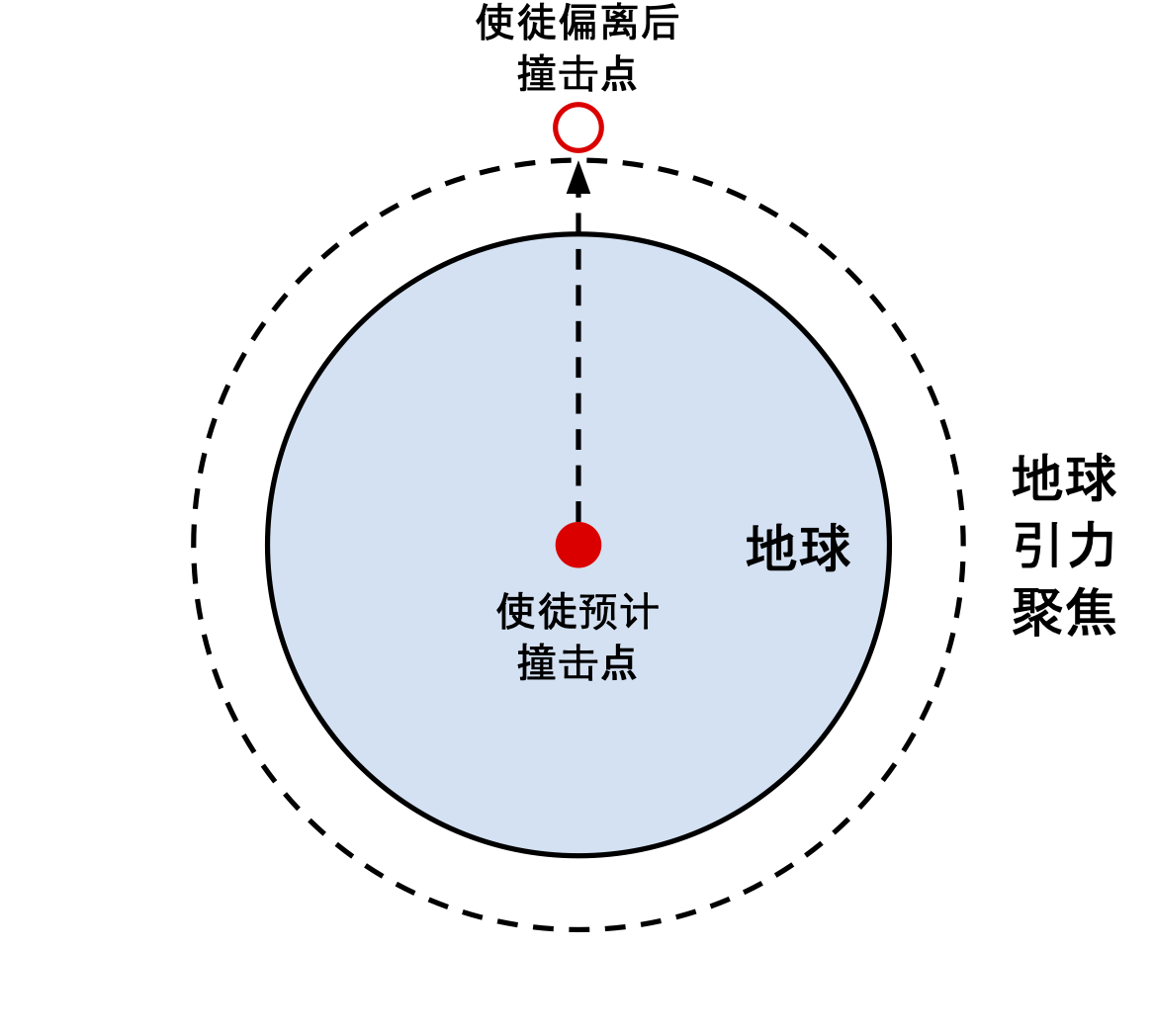「使徒袭来」示意图，考虑地球引力聚焦
带入数据后，你算得地球的引力聚焦系数为：
\[b = 1.6 R_\bigoplus\]那么，在一年的时间里，偏离使徒所需的 \(\Delta v\) 就是：
\[|\Delta v| = \frac{1.6}{3}\frac{R_\bigoplus}{T} = 0.108 \ m/s\]！！你惊讶地叫出声：原来避免人类灭绝的速度增量只需要 10.8 厘米每秒！！！
但是，最艰难的问题现在才开始：现在的人类是否有能力将一颗重达千亿吨的庞然大物推动 10.8 厘米每秒呢？
沙皇炸弹！人类最后的王牌！
压抑着自己激动的心情，你开始继续估算需要多大的能量才能将使徒推动。
使徒现在的轨道速度是：
\[v_c = \sqrt{\frac{GM}{a}} = 30\ km/s\]要给予它 \(0.108\ m/s\) 的速度增量，人类需要的能量是：
\[\begin{align*} \Delta E &= \frac{1}{2}Mv_c^2 - \frac{1}{2}M(v_c+\Delta v)^2 \\ & \approx Mv_c \Delta v \\ & = 4.24\times10^{17} \ J \end{align*}\]换算成 TNT 当量的话，这大约是 1 亿吨 TNT 爆炸的能量。你难以想象 1 亿吨 TNT 堆在一起的画面，但是却查到了人类史上的最强武器：沙皇炸弹的爆炸当量是 5 千万吨TNT！！
你看到了人类的一线生机！
不过，你还不能松懈。你考虑到氢弹爆炸时的能量是向四面八方辐射的，而要让使徒产生某一个方向的 \Delta v ，人类必须将氢弹深埋在小行星内部，并且执行精确的”定向爆破任务“。
假设一颗沙皇炸弹只有 20% 的能量能用于产生定向的速度增量，那么你需要至少 10 颗沙皇炸弹才能够完成这项看似不可能完成的任务。
你把演算用的铅笔一把拍在桌面上，身体后仰，开始呼唤助手的名字：
”助手，赶紧联系克林姆林宫，问问他们冷战时生产的沙皇炸弹还有几颗？不要听他们的什么已经销毁了之类的鬼话，我知道毛熊肯定留的有备份。人类的存亡就指望他们的炸弹了“
”还有，帮我联系世界上最有经验的爆破专家和核武专家，这回可不是定向爆破炸个楼这么简单了。楼炸歪了顶多赔钱，这使徒炸歪了可就赔命了！“
”行星安全理事会已经在协调各国航天局了对吧？嗯，动作还挺快。一个小时后我会在视频会议上汇报这次的行动方案……什么？你说理事会在问这次行动的代号是什么？“
……
”行动代号「朗基奴斯枪」“
后记
- 本文同步发表在知乎问题——「假如一颗直径为5公里的小行星正要撞向地球，人类能否逃过一劫?」；
- 文中出现的中二台本仅为增强文章的临场感使用，不代表真实情况；
- 文中公式推导来源于自己行星科学课上的课堂笔记；
- NASA 开发过一个网页小程序，可以让你直观体验如何进行“小行星防御”。