这是一个写给知乎问题——《自转的理想气体行星是什么形状的？》 的回答。
调研了一番后，我发现这是一个看似简单有趣、却极其复杂、又具有深度历史渊源的问题。
对自转天体形状的研究，可以从近代的天体物理学家钱德拉（Chandrasekhar），一路往回追溯到一大票大家耳熟能详的物理学家与数学家：洛希（Roche）、庞加莱（Poincaré）、狄利克雷（Dirichlet）、刘维尔（Liouville）、雅克比（Jocobi）、麦克劳林（Maclaurin），甚至物理学的祖师爷——牛顿（Newton）。
这篇回答主要参考了钱德拉 1969 的著作——《Ellipsoidal Figures of Equilibrium》及其他的文献。在文章的最后，我们再来看看牛顿祖师爷是怎么在自己的著作——《自然哲学的数学原理》中处理这个问题的。
截自钱德拉《Ellipsoidal Figures of Equilibrium》的目录
麦克劳林椭球（Maclaurin Spheroid）
首先，在角速度较低时，自转的理想气体行星是一个麦克劳林椭球（Maclaurin Spheroid），其表面由方程
\[{\frac {x^{2}+y^{2}}{a^{2}}}+{\frac {z^{2}}{c^{2}}}=1\]来定义，\(a\) 和 \(c\) 分别是椭球的半长轴和半短轴。椭球的偏心率 \(e\) 则定义为
\[{\displaystyle \,e^{2}=1-{\frac {c^{2}}{a^{2}}}}\]麦克劳林椭球的偏心率与天体自转角速度 \(\Omega\) 的关系如下：
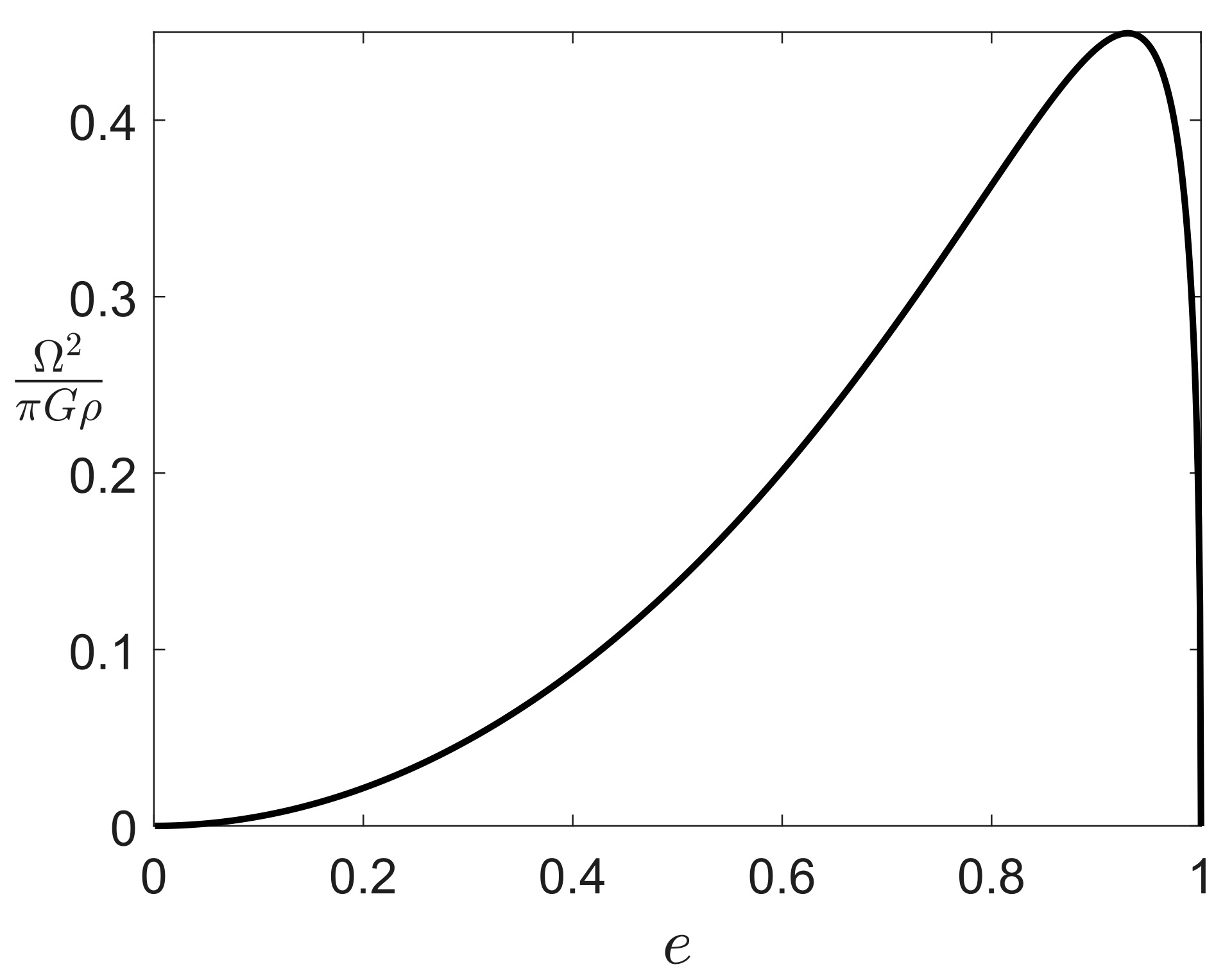
\[{\displaystyle {\frac {\Omega ^{2}}{\pi G\rho }}={\frac {2{\sqrt {1-e^{2}}}}{e^{3}}}(3-2e^{2})\sin ^{-1}e-{\frac {6}{e^{2}}}(1-e^{2})}\]其中 \(\rho\) 是天体密度，\(G\) 是引力常量。
麦克劳林椭球 | Credit: Wikipedia - Maclaurin spheroid
上图展示了椭球偏心率 \(e\) 与 \(\Omega\) 的关系。简单来说，行星的自转速度越快，形状就会越椭，这十分符合我们直观上的认知；此外，我们还可以看到，麦克劳林椭球的偏心率在 \({\displaystyle \Omega ^{2}/(\pi G\rho ) > 0.449331}\) 的地方（图上的峰值）是没有定义的，这就意味着，当行星旋转太快后，平衡状态消失，行星将无法维持稳定的椭球形状。
雅克比椭球（Jacobi ellipsoid）
麦克劳林于 1742 年建立起自旋天体形状的相关理论，在之后近一个世纪的时间里，人们都以为该问题只有这一个绕转轴对称的解。甚至，拉格朗日在重新探究了这个问题的数学方程后，都认为椭球的两条轴应该是相等的。但是，在 1834 年，雅克比发现这个问题居然还有一个非对称的三轴椭球解！方程如下：
\[{\displaystyle {\frac {\Omega ^{2}}{\pi G\rho }}=2abc\int _{0}^{\infty }{\frac {udu}{(a^{2}+u)(b^{2}+u)\Delta }}\ ,\quad \Delta ^{2}=(a^{2}+u)(b^{2}+u)(c^{2}+u);}\] \[{\displaystyle a^{2}b^{2}\int _{0}^{\infty }{\frac {du}{(a^{2}+u)(b^{2}+u)\Delta }}=c^{2}\int _{0}^{\infty }{\frac {du}{(c^{2}+u)\Delta }}.}\]用上述方程解得的 \(a, b, c\) 还满足不等式：
\[{\displaystyle {\frac {1}{c^{2}}}>{\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}.}\]也就是旋转轴一定是最短轴 \(c\)，而指向赤道的两根轴则长度不一样。
你可能要问：旋转如此奇异的天体在现实中真的存在吗？
实际上，鸟神星 Haumea 就是一颗雅克比椭球。2010 年，通过分析鸟神星的亮度变化曲线，天文学家发现鸟神星的三轴长度分别为 1920 * 1540 * 990 km，而它正在绕着自己的最短轴旋转（Lellouch et al. (2010)）。
鸟神星的旋转 | Credit: Wikipedia - Haumea
在随后的 1842 年和 1846 年，Meyer 和刘维尔证明了在轴对称椭球的偏心率超过 \(0.812670\) 后，相同角动量的三轴椭球具有更低的总能量。也就是说，如果天体的内部有能量耗散机制的话，那么大偏心率的轴对称麦克劳林椭球将会逐渐演化成一个非对称的雅克比椭球，很神奇对吧！这种数学现象后来被庞加莱称为“分岔（Bifurcation）”。
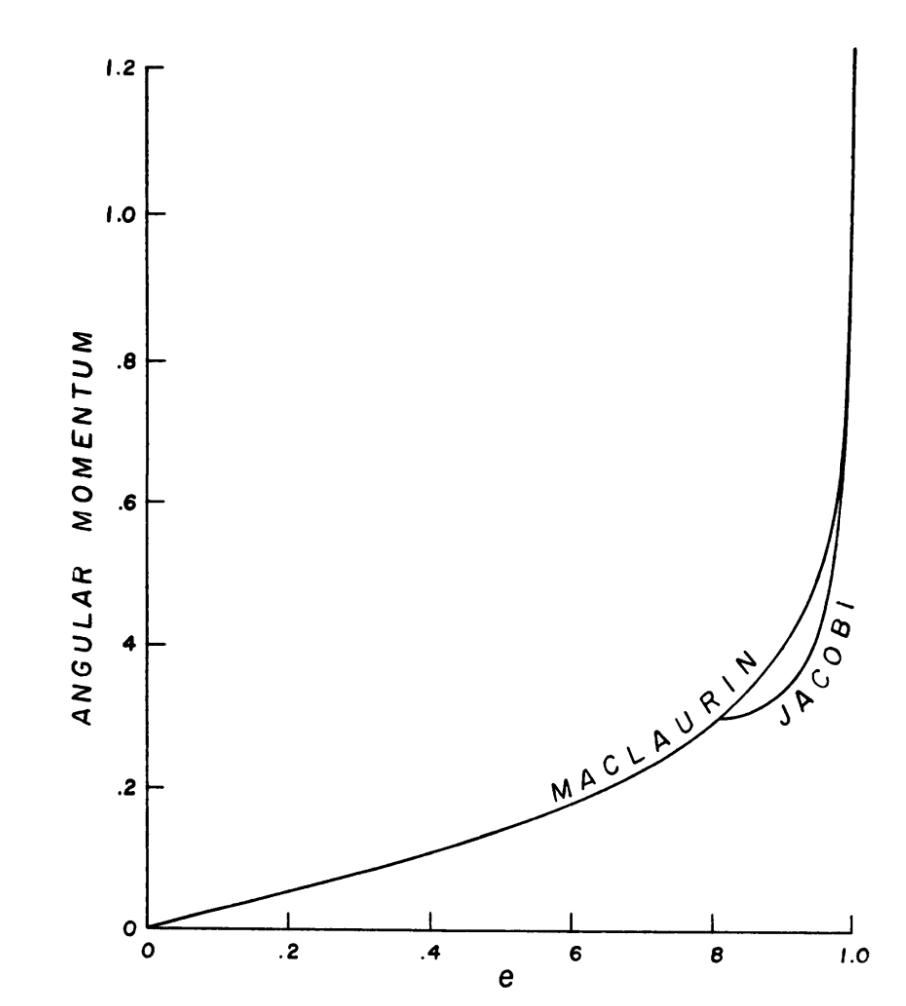麦克劳林椭球到雅克比椭球的分岔 | Credit: 钱德拉《Ellipsoidal Figures of Equilibrium》
戴森-王甜甜圈（Dyson-Wong toroid）
然而，这个问题的神奇之处还不止于此：
自转的理想气体行星可以不是球形的，它甚至可以是甜甜圈！
1974 年，Wong 发现了除了麦克劳林椭球之外，这个问题还存在一个环形的轴对称稳定解。现在这个解被称为 Dyson-Wong toroid（戴森-王甜甜圈，自己起的译名，仅供参考）。
注：这里的戴森不是提出“戴森球”的弗里曼·戴森，而是弗兰克·戴森。根据维基百科，虽然不确定两人是否是有亲戚关系，但是弗里曼·戴森相信弗兰克·戴森激发了他对天文学的兴趣。
随后，又有研究者发现，戴森-王甜甜圈也是可以从麦克劳林椭球分岔过去的（Eriguchi & Sugimoto (1981)）。下图就展示了如何从一个自转的椭球体“过渡成”一个自转的甜甜圈。
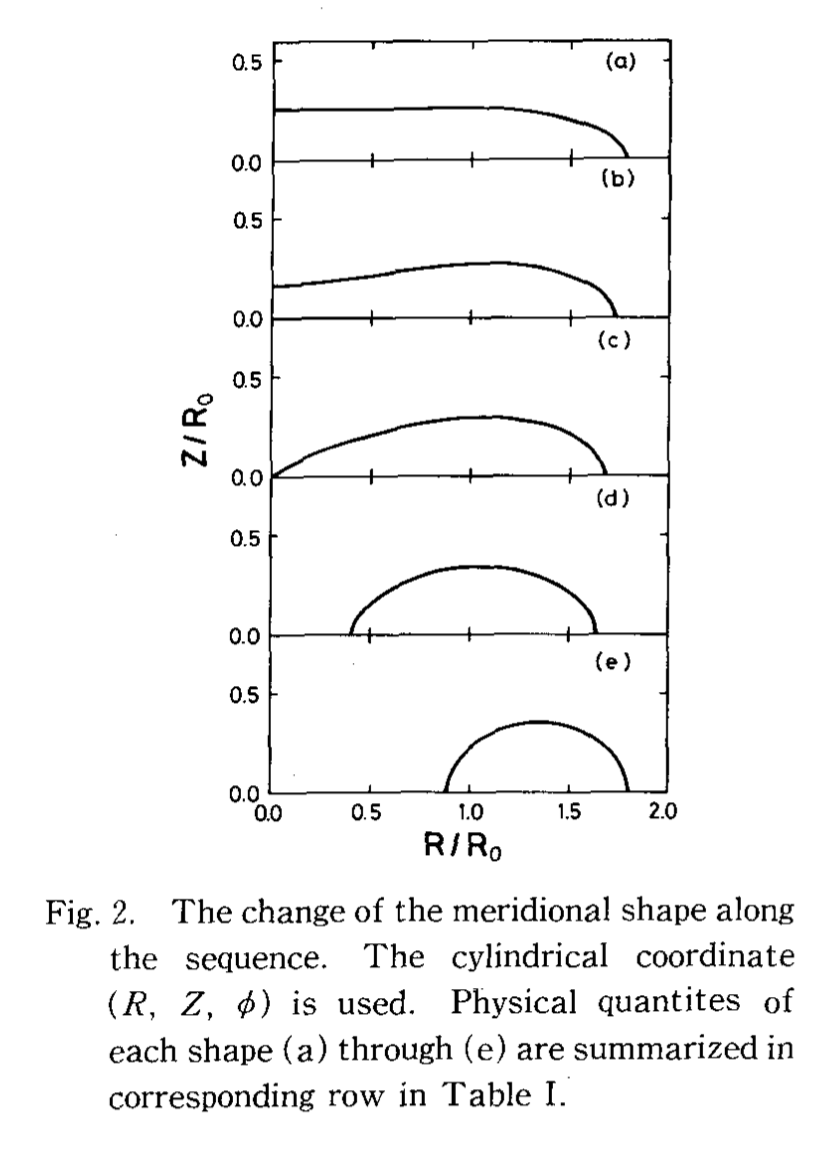麦克劳林椭球到戴森-王甜甜圈的分岔 | Credit: Eriguchi & Sugimoto (1981)
所以，下面这样的甜甜圈星球在理论上也是可以存在的勒：
也许甜甜圈地球真的可能存在
祖师爷的解法
关于自旋天体形状的研究，早在牛顿的巨作——《自然哲学的数学原理》就已经出现了。牛顿用一个非常直观的方法，推导出了自旋天体的扁率和角速度的关系。这里，我参考了钱德拉翻译的《Newton’s Principia for the Common Reader》，来看看牛顿是怎么处理这个问题的：
牛顿上来就把地球钻出了两条隧道，一条从地心通往极点，另一条从地心通往赤道，又把隧道都灌满水。
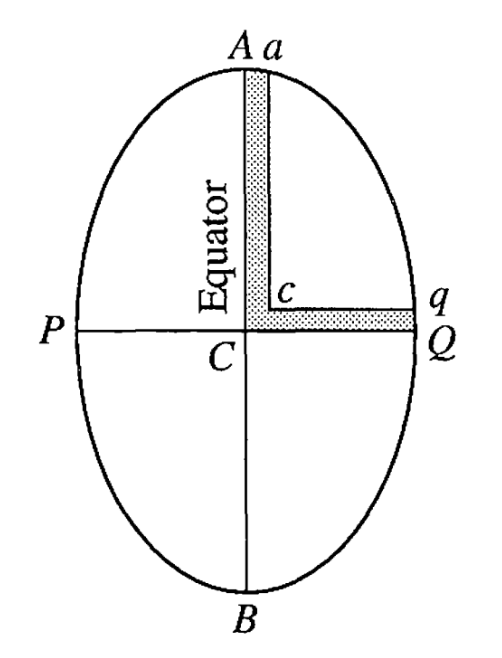从地心向赤道和向极点挖的两条隧道，并灌满水 | Credit: 《Newton’s Principia for the Common Reader》
这两条隧道的长度分别是地球椭球的半长轴 \(a\) 和半短轴 \(b\)。若地球半径为 \(R\)，那地球的扁率则为：
\[\epsilon = \frac{a-b}{R}\]定义 \(m\) 为赤道处向心加速度与地球表面平均加速度的比值：
\[m = \frac{\Omega^2 R}{GM/R^2} = \frac{\Omega^2 R^3}{GM}\]那么赤道隧道中水的总重量为：
\[\text{weight} = \frac{1}{2} \rho a g_\text{eq} (1-m)\]而极隧道中水的总重量则为：
\[\text{weight} = \frac{1}{2} \rho b g_\text{pole}\]因为液体平衡，两边隧道中水的重量必须相等（其实就是流体静力学平衡）：
\[a g_\text{eq} (1-m) = b g_\text{pole}\]用 \(b=a(1-\epsilon)\) 变量替换，得到：
\[\begin{align*} {g_\text{pole} \over g_\text{eq}} = \frac{a}{b}(1-m) &= \frac{1-m}{1-\epsilon} \\ &\approx (1+\epsilon-m) \end{align*}\]在这本书的前面，牛顿就已经推出了椭球主轴上的重力加速度可以近似为：
\[\begin{align*} g_\text{pole} &\approx \frac{4}{3}\pi a(1-\frac{1}{5}\epsilon) \\ g_\text{eq} &\approx \frac{4}{3}\pi a(1-\frac{2}{5}\epsilon) \end{align*}\]那么行星的扁率即为：
\[\epsilon = \frac{5}{4}m = \frac{5\Omega^2 R^3}{4GM} = \frac{15\Omega^2}{16\pi G\bar{\rho}}\]这个结果正是麦克劳林椭球解小偏心率情况下的展开，感兴趣的读者留作课后习题自己证明。
使用这个公式，牛顿算出了地球的扁率是 \(1 \over 230\)，而木星的扁率是 \(1 \over 9.25\)；这比地球的实际扁率 \(1\over 298\) 和木星的实际扁率 \(0.065\) 都要大，这主要是由于地球、木星的非均匀密度导致的。
这就是牛顿的解法。
It is so elegant. So intelligent. —— T.S. Eliot